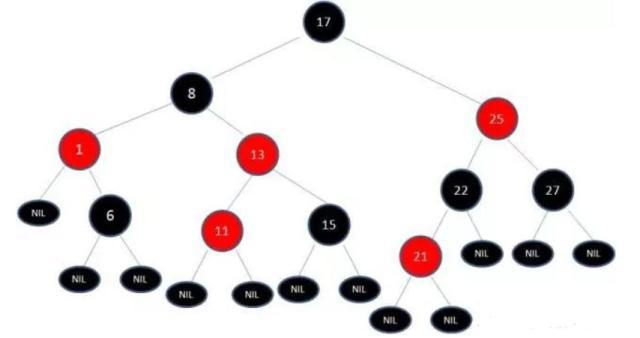
红黑树是一种特定类型的二叉树 ,它是在计算机科学中用来组织数据比如数字的块的一种结构。若一棵二叉查找树是红黑树,则它的任一子树必为红黑树.
红黑树是一种平衡二叉查找树的变体,它的左右子树高差有可能大于 1,所以红黑树不是严格意义上的平衡二叉树 (AVL),但 对之进行平衡的代价较低, 其平均统计性能要强于 AVL 。
由于每一颗红黑树都是一颗二叉排序树,因此,在对红黑树进行查找时,可以采用运用于普通二叉排序树上的查找算法,在查找过程中不需要颜色信息。
恢复红黑树的属性需要少量(O(log n))的颜色变更(实际是非常快速的)和不超过三次树旋转(对于插入操作是两次)。 虽然插入和删除很复杂,但操作时间仍可以保持为 O(log n) 次 。
特征:
节点是红色或黑色。
根节点是黑色。
所有叶子都是黑色。(叶子是NUIL节点)
每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
https://www.cnblogs.com/gofighting/p/5437998.html
https://baijiahao.baidu.com/s?id=1641940303518144126&wfr=spider&for=pc
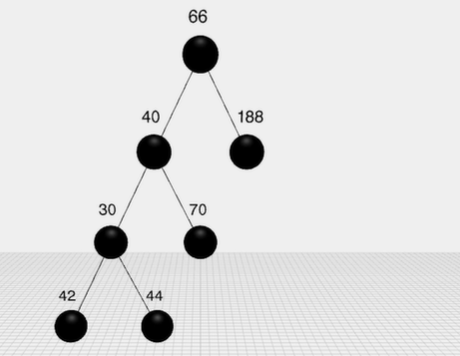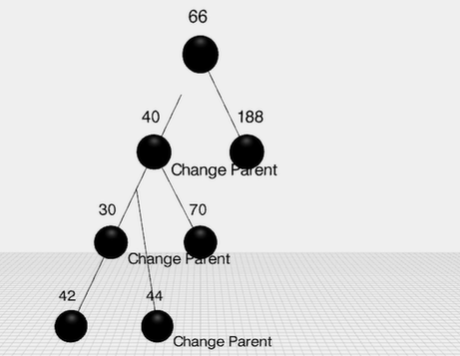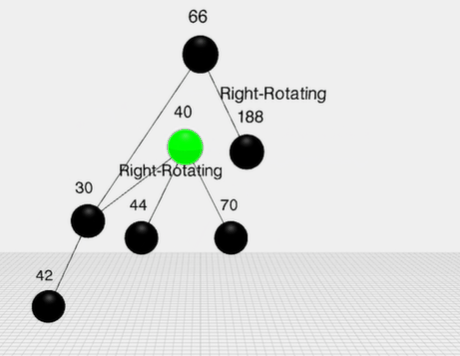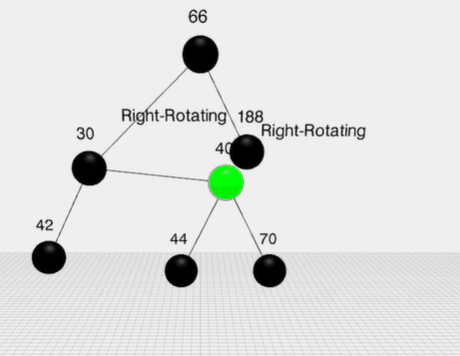
标准的二叉树: 右子节点比父节点大,左子节点比父节点小,查找的时候就实现了折半查找了
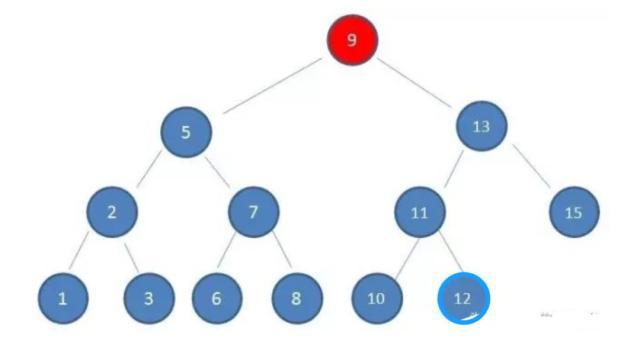
每次插入和删除时,都会改变树的结构,此时可能会破坏红黑树的规则,则有两种操作来继续保持规则—-变色,(左/右)旋转
变色: 把红变黑, 或者黑变红,(尽可能的使其符合规则)
旋转: 变色不能满足时,则通过旋转,看图
左旋:
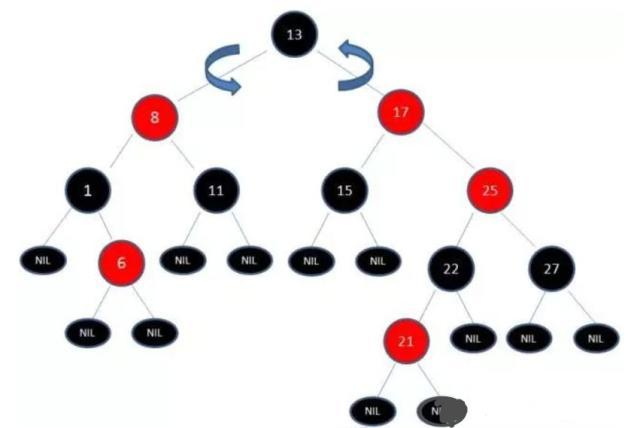
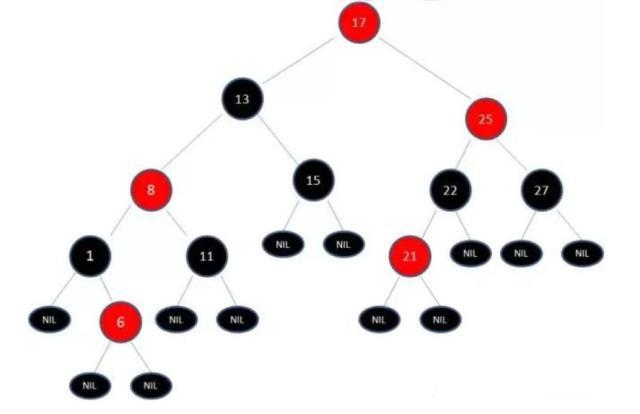
变成了
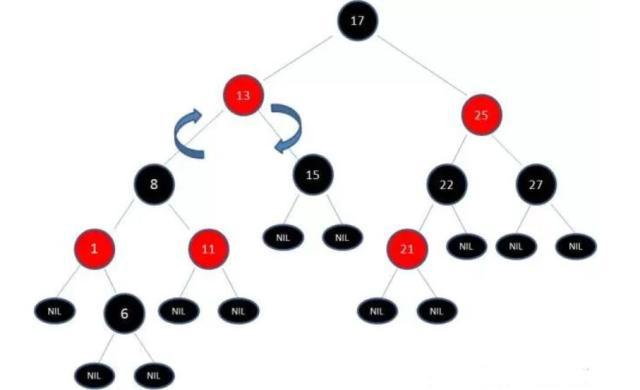
右旋转:
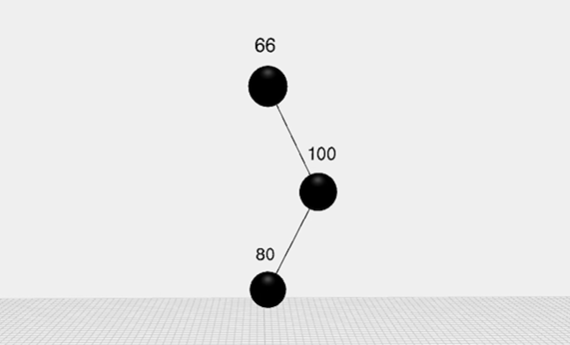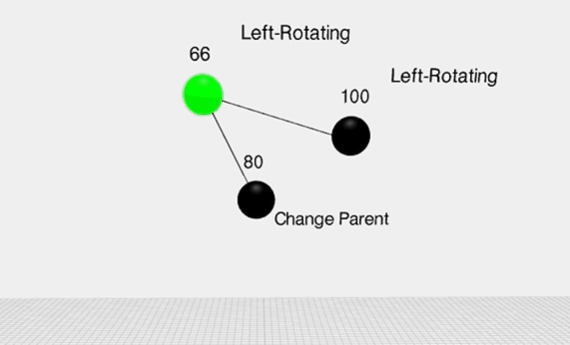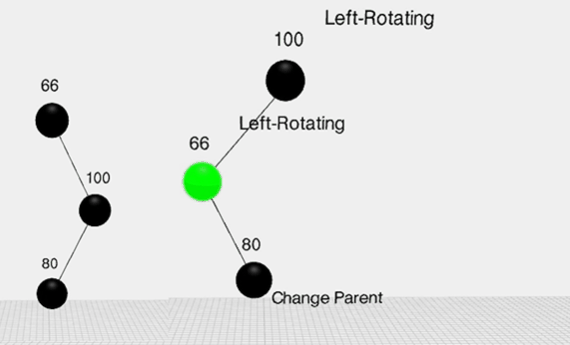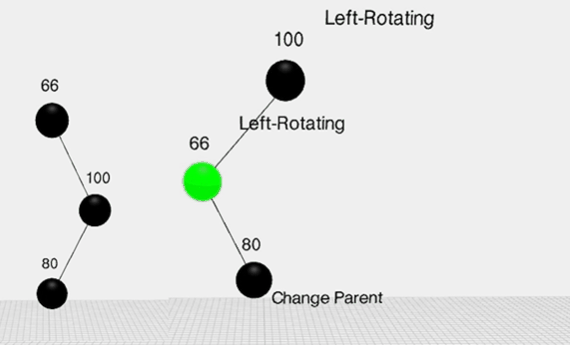
变成了